[GAME] Pacman - AI!

Pacman, this was basically to test out my new path finding algorithm I wrote for Lua;

Usage, [] are optional:

pacman [scale] [speed]

By default scale is 1 and speed is 0.2, this is how fast the game updates and scale is how big the tiles are (makes the game run worse)

A maximum of 4 ghosts are there at a time, they spawn every 5 seconds, how the AI works:
The ghosts will travel to your last position, when they arrive there they go to your new last position etc.

How you move: use left/right/up/down arrow keys.

Screenies:

Spoiler

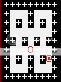
Download:

Spoiler

http://pastebin.com/sW6BFpMK

Tell me what you think, feel free to look at or use the pather :P/>

Really nice game (even though it's at its infancy), I enjoyed it but on my screen in ComputerCraft (25x62) it's kinda hard to play.

Cool game bro.

Awesomesauce.

Very cool!

Sort of related to this post, Pac-Man is an interesting case in early artificial intelligence. If I remember correctly, the ghosts only computed paths when reaching intersections in the map- two would always move in the direction of Pac-Man, one would predict the intersection in front of Pac-Man and try to move towards that (so as to cut him off), and one would always choose a random direction to move in, as a sort of roving obstacle.

I was browsing the subject and came across this surprisingly interesting paper: http://nlp.cs.berkeley.edu/pubs/DeNero-Klein_2010_Pacman_paper.pdf

Your implementation of node-based pathfinding looks solid. I didn't see any weights or heuristics being used in your pathfinder, but you may have included them. If so, and you're going with the pacman maze structure, you could optimize it by adding weights to each pathway and only using intersections as nodes- this could reduce a 50x50 map down to maybe 20,30 nodes.

But I'm probably looking in too much detail, just a thought-provoking post. Thanks for sharing BillysBack!

nitrogenfingers, on 04 December 2012 - 01:46 PM said:

Very cool!

Sort of related to this post, Pac-Man is an interesting case in early artificial intelligence. If I remember correctly, the ghosts only computed paths when reaching intersections in the map- two would always move in the direction of Pac-Man, one would predict the intersection in front of Pac-Man and try to move towards that (so as to cut him off), and one would always choose a random direction to move in, as a sort of roving obstacle.

I was browsing the subject and came across this surprisingly interesting paper: http://nlp.cs.berkeley.edu/pubs/DeNero-Klein_2010_Pacman_paper.pdf

Your implementation of node-based pathfinding looks solid. I didn't see any weights or heuristics being used in your pathfinder, but you may have included them. If so, and you're going with the pacman maze structure, you could optimize it by adding weights to each pathway and only using intersections as nodes- this could reduce a 50x50 map down to maybe 20,30 nodes.

But I'm probably looking in too much detail, just a thought-provoking post. Thanks for sharing BillysBack!

NitrogenFingers - making the rest of us looking like gibbering baboons since his first post ;)/>

But on topic, very nice job with the path-finding. I haven't really sorted through it all yet, but from what I've seen it is very solidly coded.

Earlier to day I was thinking about the algorithm I used to find the paths and thinking of ways to add "costs" to moving in certain directions, The way I figured I could use them is by dividing the todo list up by priority, with priority being the map ID + 1 (so 0 would be 1), then only performing the spreading of the tiles in the todo list with the lowest priority, this would mean that if you wanted "0" to be the prioritized route then it would try taking that, but if 0 led to no solutions then it would work through occurrences of 1. The only thing wrong with this would be that not only would the extensions of 0 stack up in the priority list of 1 meaning that lot's of irrelevant paths would be checked once priority 0 was found to lead to no solutions but the path finder would over-prioritise lower values paths, a path consisting of S-0-1-E would be worse than S-0-0-0-0-0-0-0-0-0-E where S = start and E = end.

I can't really think of another way of adding costs of tiles in to this algorithm however…

and thanks for all of the compliments :D/>

also, for those interested here's a basic note on how the algorithm works:

Spoiler

It has two tables, done and todo, it loops through todo on each loop and gets the tiles on all 4 sides of the origin tile, It then checks this tile against the "done" list and against the map, only adding it if the tile ID is equal to 0. If it works then it adds a new value to the done list, a table containing x, y, and origin. The origin is the tile that this was a side of.
The loop stops when either the todo list is found to be empty (all possible tiles were searched) or the target was found, the resulting tile table (x, y, origin) is then set as the "result". The result is then looped through, resetting the current tile as the origin on each loop until the origin equals nil (this is then the start), on each loop of the result the tile's {x, y} is added to the path.
The way this loop works means that the path is returned in reverse order, so I created the "flipTable" function below the "findPath" function to get the path in the correct direction.

I guess what I could do is simplify the map down using and algorithm to detect and void all strait lines, only adding data to the map when the next node appears and in the correct way, so that the map is squashed so that there are no unnecessary corridors. Then add data to the node to inform the game of the distance between the nodes so that the game can add the nodes back in again, this would involve a slight re-write of the current path finder and it may be difficult to keep the accuracy of the map with this node map, it would have to have an easy way of getting nodes above, below and to the sides of the current node (if they exist)

Update;
Updated the AI so that it has a 1/2 chance of re-routing to the player if it reaches an intersect and a 1/4 chance of making a random path instead of pathing to the player. The second one is because I found the ghosts making trains and doing the exact same thing, some randomization was needed to muddle things up :P/> Also there is some new usage, you can set the scale of the board and the speed at which the game plays. It also tells you your score when you game over.

This post is mostly me rambling so I'll put it in spoilers:

Spoiler

In regards to weighting paths I was considering an A* algorithm. The technique there is by providing a score S to each open node according to:
S = G + H
Where G is the distance from the starting point to that particular node, and H is the heuristic measure (an "as the crow flies" travel distance). When determining which node to check from the open list you always choose the one with the lowest score, thus ensuring that your path is as straight as possible. Of course it depends on the environment- this may not be well suited to complex mazes with lots of dead ends for example, there a breadth first search would be more appropriate, and so on.
The classical implementation of a weighted path find in video games is of course tiled environments, but it's history is in solving graph theory problems and works just as well on a connected graph- an environment that PacMan lends itself to very well. Consider the PacMan maze:

We can consider each intersection to be a node in a graph, and the passageway between them a connection between nodes. In creating this representation I would probably do a parse of the game world from top to bottom- for each tile in the game world if it has 3 or more open tiles adjacent to it, it is considered an intersection and added to that list. Once all intersections had been located you could one by one follow each path from the intersection and link them to other intersections in the list- the distance between nodes, IE the number of times plus a cost for turning if you game includes that, is the weight for that passage:

If we're trying to get our ghost to move, we'll probably be considering intersections, the closest one to the player in terms of distance. So the problem becomes trying to find the shortest path from one intersection to the next. So you could calculate a heuristic value for each for each intersection by guessing roughly how far from each intersection to the target the ghost would need to travel, but you might find the heuristic to be too inaccurate. The alternative is to use a shortest path algorithm like Dijkstra's Algorithm, considering every node and always taking the shortest available path on your considered graph until you reach the target.

The cool thing about Pac Man is imperfect paths aren't necessarily a bad thing, as the search space is quite small and they're looking for broad intersections, not specific ones. In fact if 3 ghosts starting from 3 points moving towards a corner end up picking 3 different intersections you've given the player a challenging scenario, one most Pac Man players will be familiar with. Having a perfect path chosen will lead to the ghosts following the player in a long conga line, which is nowhere near as interesting or as challenging.

It's a fantastically interesting problem, the PacMan AI problem…

nitrogenfingers, on 05 December 2012 - 12:14 PM said:

This post is mostly me rambling so I'll put it in spoilers:

Spoiler

In regards to weighting paths I was considering an A* algorithm. The technique there is by providing a score S to each open node according to:
S = G + H
Where G is the distance from the starting point to that particular node, and H is the heuristic measure (an "as the crow flies" travel distance). When determining which node to check from the open list you always choose the one with the lowest score, thus ensuring that your path is as straight as possible. Of course it depends on the environment- this may not be well suited to complex mazes with lots of dead ends for example, there a breadth first search would be more appropriate, and so on.
The classical implementation of a weighted path find in video games is of course tiled environments, but it's history is in solving graph theory problems and works just as well on a connected graph- an environment that PacMan lends itself to very well. Consider the PacMan maze:

We can consider each intersection to be a node in a graph, and the passageway between them a connection between nodes. In creating this representation I would probably do a parse of the game world from top to bottom- for each tile in the game world if it has 3 or more open tiles adjacent to it, it is considered an intersection and added to that list. Once all intersections had been located you could one by one follow each path from the intersection and link them to other intersections in the list- the distance between nodes, IE the number of times plus a cost for turning if you game includes that, is the weight for that passage:

If we're trying to get our ghost to move, we'll probably be considering intersections, the closest one to the player in terms of distance. So the problem becomes trying to find the shortest path from one intersection to the next. So you could calculate a heuristic value for each for each intersection by guessing roughly how far from each intersection to the target the ghost would need to travel, but you might find the heuristic to be too inaccurate. The alternative is to use a shortest path algorithm like Dijkstra's Algorithm, considering every node and always taking the shortest available path on your considered graph until you reach the target.

The cool thing about Pac Man is imperfect paths aren't necessarily a bad thing, as the search space is quite small and they're looking for broad intersections, not specific ones. In fact if 3 ghosts starting from 3 points moving towards a corner end up picking 3 different intersections you've given the player a challenging scenario, one most Pac Man players will be familiar with. Having a perfect path chosen will lead to the ghosts following the player in a long conga line, which is nowhere near as interesting or as challenging.

It's a fantastically interesting problem, the PacMan AI problem…

NitrogenFingers….. You think WAAAAAYYY too much O.O
You did this post on a whim, and made it look like a professional news article. STOP BEING SO AWESOME!

Spoiler

But in reality, I enjoyed reading that. +1 for you, sir!

nitrogenfingers, on 05 December 2012 - 12:14 PM said:

This post is mostly me rambling so I'll put it in spoilers:

Spoiler

In regards to weighting paths I was considering an A* algorithm. The technique there is by providing a score S to each open node according to:
S = G + H
Where G is the distance from the starting point to that particular node, and H is the heuristic measure (an "as the crow flies" travel distance). When determining which node to check from the open list you always choose the one with the lowest score, thus ensuring that your path is as straight as possible. Of course it depends on the environment- this may not be well suited to complex mazes with lots of dead ends for example, there a breadth first search would be more appropriate, and so on.
The classical implementation of a weighted path find in video games is of course tiled environments, but it's history is in solving graph theory problems and works just as well on a connected graph- an environment that PacMan lends itself to very well. Consider the PacMan maze:

We can consider each intersection to be a node in a graph, and the passageway between them a connection between nodes. In creating this representation I would probably do a parse of the game world from top to bottom- for each tile in the game world if it has 3 or more open tiles adjacent to it, it is considered an intersection and added to that list. Once all intersections had been located you could one by one follow each path from the intersection and link them to other intersections in the list- the distance between nodes, IE the number of times plus a cost for turning if you game includes that, is the weight for that passage:

If we're trying to get our ghost to move, we'll probably be considering intersections, the closest one to the player in terms of distance. So the problem becomes trying to find the shortest path from one intersection to the next. So you could calculate a heuristic value for each for each intersection by guessing roughly how far from each intersection to the target the ghost would need to travel, but you might find the heuristic to be too inaccurate. The alternative is to use a shortest path algorithm like Dijkstra's Algorithm, considering every node and always taking the shortest available path on your considered graph until you reach the target.

The cool thing about Pac Man is imperfect paths aren't necessarily a bad thing, as the search space is quite small and they're looking for broad intersections, not specific ones. In fact if 3 ghosts starting from 3 points moving towards a corner end up picking 3 different intersections you've given the player a challenging scenario, one most Pac Man players will be familiar with. Having a perfect path chosen will lead to the ghosts following the player in a long conga line, which is nowhere near as interesting or as challenging.

It's a fantastically interesting problem, the PacMan AI problem…

Is this not essentially what I suggested;

Spoiler

(this is an idea, not what actually happens)
The map consists not tile by tile but intersect by intersect, with each node having a few child nodes, each with different values, and you follow these trees adding up the values until all of your node trees stop.
The only problems I can see with this is that unless you wanted to presume that the first node path to get to your target node was the fastest you would theoretically need to search through every node and get every possible path from the starting point of the path, this may end up making the path finder less efficient than a simple spreading path finder. Also you would need a sub path finder in order to find the distance between two intersect, obviously nodes can be initialized when the map is instead of every time you search for a path but this would still require another path finder.

Another route I could take is adding presumptions to my path finder; In other words I would presume that the shortest path I could find would be in the general direction of that path, and only let the path stray a few tiles away from this direct path. This would mean that in some cases it would create a more efficient path finder but at the cost of slowing down more complex paths.

I looked up the word "Heuristic" by the way, and couldn't find a very good explanation for it in terms of path finding, an explanation would be appreciated :P/>

either way you made very good points :D/>

Once again we'll do this in spoilers (I hope I'm not side-tracking the discussion)

Spoiler

When we're talking about either A* or Dijkstra's, we don't have to worry about our path being sub-optimal, because the scoring is what we use to ensure the path is optimal. I'll explain as I go.

So the equation I showed earlier, S = G + H, where S is the "score" for any given node in our list, G is the distance from the Start Node and H is our Heuristic. To deconstruct, G is how many tiles in the current path we would need to travel to get to the currently checked tile. If the tile is adjacent to the ghost for example, then G = 1, as it's 1 tile's distance. H is referred to as a heuristic, which is a fancy way of saying it's a guess as to how optimal the path is. Typically it's measured by taking the absolute distance between our selected node and the end point, assuming this is how far we'd need to travel if there's nothing blocking the path. By including the heuristic measure, we can provide an assessment on which path appears to be moving in the correct direction. For example:



So I've just made a quick example here where a given start node (red) is 5 units of distance away from our goal node (green). In our open node list there are four possible moves- left, right, up and down. When we make these nodes I've also included the two measures that give them their score- G for our path distance and H for our heuristic measure. A* should always choose the node with the lowest score first, with the choice for equally scored nodes being arbitrary. In that case you can see the first node A* has to pick is the one to the right, as it has the lowest score of 5 compared to 5 /2 and 7 for the other nodes. There may be an obstruction that makes that heuristic incorrect, but we can't assume that, nor can we assume what is the best path for a given situation without testing- our heuristic measure simply makes sure we're testing the most promising options first. This means with A* (unlike Dijkstra's) we don't need to worry about other suboptimal paths as we always take the lowest cost path first- that means the second we arrive at our target we're guaranteed to have the lowest cost path as every other path is provably equal or higher in cost.

If you're unsure, a good way to do this is to trace it out. Follow it from start to finish- you might find especially with a small obstruction you'll explore paths above or below, or even behind the node first but eventually the best or equal-best path will be the one that's produced.

In regard to the distance between two intersections, I would do this in the pre-game parsing, when intersections are first identified. You would simply follow the path for each intersection, and when you reach another intersection, identify it and add the distance and that intersection to the definition of the existing intersection. This forms a connection in our graph, and has a one-time cost as opposed to having to use a path-finder between intersections- there's only one path so there's no need to path find :)/>/> The algorithm for travelling between intersections is very easy- from the initial facing keep moving until you you either reach the next intersection or a corner- in which case turn in the direction that is not backwards and keep going.

Of course I can only provide a cursory explanation in this context- there is much more detail about this on the web.