Trigonometry and Me - The love-hate relationship

I'm not sure if this post should go in general, or this topic. It's not specifically about CCLua -

So i've been browsing different neat looking code snippets from multiple languages. Which usually consists of me looking at the source, going "Hey I understand this!" Then coming across math.cos, math.sin, math.tan and so on and basically rage quitting my text editor.

I've looked up some trig guides, but they kind of just give you the information and send you on your way.

What i'm trying to get at is can anybody send me to some good links/guides that can help me apply trig concepts to coding? Or even help me out yourself? (Don't feel obligated by any means)

Thanks a lot, - X

Also: 100th post, woo.

Although the only time I've really used those functions was in my freshman geometry class, so I might not be of too much help.

The most appropriate way that I can think of for you to apply these concepts is in graphics when working with triangles. In the class that I took, we used the relationships between sine, cosine, and tangent in order to find lengths of sides of a triangle. This link might help you with that.

I'm French and I know a wonderful site about learning informatics and related from scratch. Though in French, maybe you can understand math things (there are plenty of trigo tuto on this site, some with less talk and more math, but as far as it is for beginners, there are a lot of useful explanation… in French. I took the one I think is the better,but you can googlize "site du zero trigonometrie" for the others. I didn't tried to google translate it, so I don't know if it's understandable).

Here is a discussion about English equivalents of this site. I sorted the most relevant sites I saw:

Spoiler

http://stackoverflow.com
http://forums.asp.net/
http://www.codecademy.com/

The two first are forums, so you should consult them with precise questions in mind. I just discovered the last one and I guess you may not know it. It just is AMAZING: interactive, pedagogic and all. Well, I just saw their tutorial for trigonometry with Jscripts, and I think I've been a bit too excited ; this tuto is wrong about the area of a triangle, so, you'd better not go there.

Well, I didn't found yet any English tuto at the level of the one on the site du zeros, but I'll search a bit.
One thing useful I haven't found on the few tutos I saw is how to compute the angles between a vector u and a vector v?
we have u.v = |u||v| cos(u;v)
and |u^v| = |u||v| |sin(u;v)| which is also twice the area of the triangle ABC if AB = u and AC = v

the second I read the first post… My math teachers voice appeared in my head going "sohcahtoa" :D/>

the problem was I could not remember which side was which on the triangle. lol.

I did not know how to use many of the math tools, but this site for lua has a breif description of them all …

http://lua-users.org/wiki/MathLibraryTutorial

http://www.lua.org/pil/18.html

http://www.gammon.com.au/scripts/doc.php?general=lua_math


while looking at these… lua will give you a different result to a calculator.. as a calculator works in degrees, lua works in radians. (radians = degrees * pi / 180)

I would recommend coming up with a problem you need to solve with trig and then asking for help with it. that is the easiest way to teach it I reckon

The easiest way to understand basic trigonometry it to understand how the Sin, Cos and Tan functions came to be. (Something not taught in most maths classes).

Spoiler

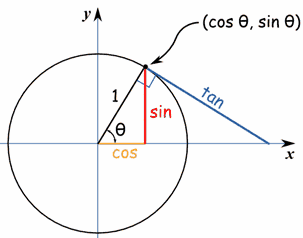
Sin,Cos and Tan derive from the concept of a unit circle- a circle with a radius of 1.
A line the length of 1, drawn on the circle will have an angle, dubbed Theta (θ).
The sine of the angle (theta) is the Y co-ordinate of the point where the line touches the circle.
The cosine of the angle (theta) is the X co-ordinate of the point where the line touches the circle.
From knowing the line's start point (0,0), its end point (Cos θ, Sin θ) and its angle, it's possible to define a triangle.
It is because of this that Sin and Cos are capable of determining facts about a triangle.

Tan is slightly different in that it is the length of the straight line that joins the X and Y axes with the point where the line touches the circle.

In addition, the following rule apply:

Spoiler

These equations can be used to fill in the blanks for triangles with missing data.
By applying inverse operations (like o = h * Sin θ).

There are of course two ways of measuring angles - degrees and radians, most computer implementations use radians because they're easier for the computer to work with, CC lua is no exception. Luckily CC's math api defines a rad function to convert degrees to radians (and a deg function for the opposite)

Hopefully that clears up the basics.

Thank you to all who replied, you've all been very helpful!

Also, This helped me apply my trig understanding to use in lua/any other language.

http://inventwithpyt...ns-at-a-target/

Edit: After messing around a bit in LÖVE I managed this (Not impressive, but progress!)

Just to hopefully give you and others a better understanding (if it's needed), I thought up a simple scenario.

Imagine you are standing on top of the center of an XY graph, facing directly "up" the Y axis (or north). You have a heavy rock, which you can throw exactly 1 meter away from you. If you turn 40 degrees to your right and throw the rock, the position of the rock is (sin(40), cos(40)), approximately (0.64, 0.77). If you keep turning another 50 degrees (bringing you to 90 degrees) and throw another rock, the position of the second rock is (sin(90), cos(90)), exactly (1, 0).

More formally, sin(θ) and cos(θ) give the x and y components of the point 1 unit away from (0, 0) at the angle θ.