2679 posts
You will never find me, muhahahahahaha
Posted 12 January 2016 - 08:31 PM
Hello guys,
during the last few days I have been experimenting with bezier curves and drawing fonts with them. At this point I can generate the path by iterating from 0 to 1 at a given interval. The result is satisfying and it works. However, for filling bezier polygons made of bezier curves and segments, I need a mathematical function that will give me the intercepts of a curve at a given y-coordinate. First, here is a comparison between both methods:
On the left side you can see an "a" generated by getting the path (the method that iterates from 0 to 1) and on the left I iterate from top to bottom and check if the beziers and segments intercept the given row. In this screenshot I have disabled the lines.
On this screenshot only the line are being rendered.
Here I render beziers and curves at the same time.
What should I do to make it generate the same form on the right and left sides?
The code I am currently using for the bezier curves.
The code used for segments:
And the code I use for the drawing itself:
Finally, a special note to Bomb Bloke. I used this website.
Thanks in advance guys!
Edit: Please go the 10th answer.
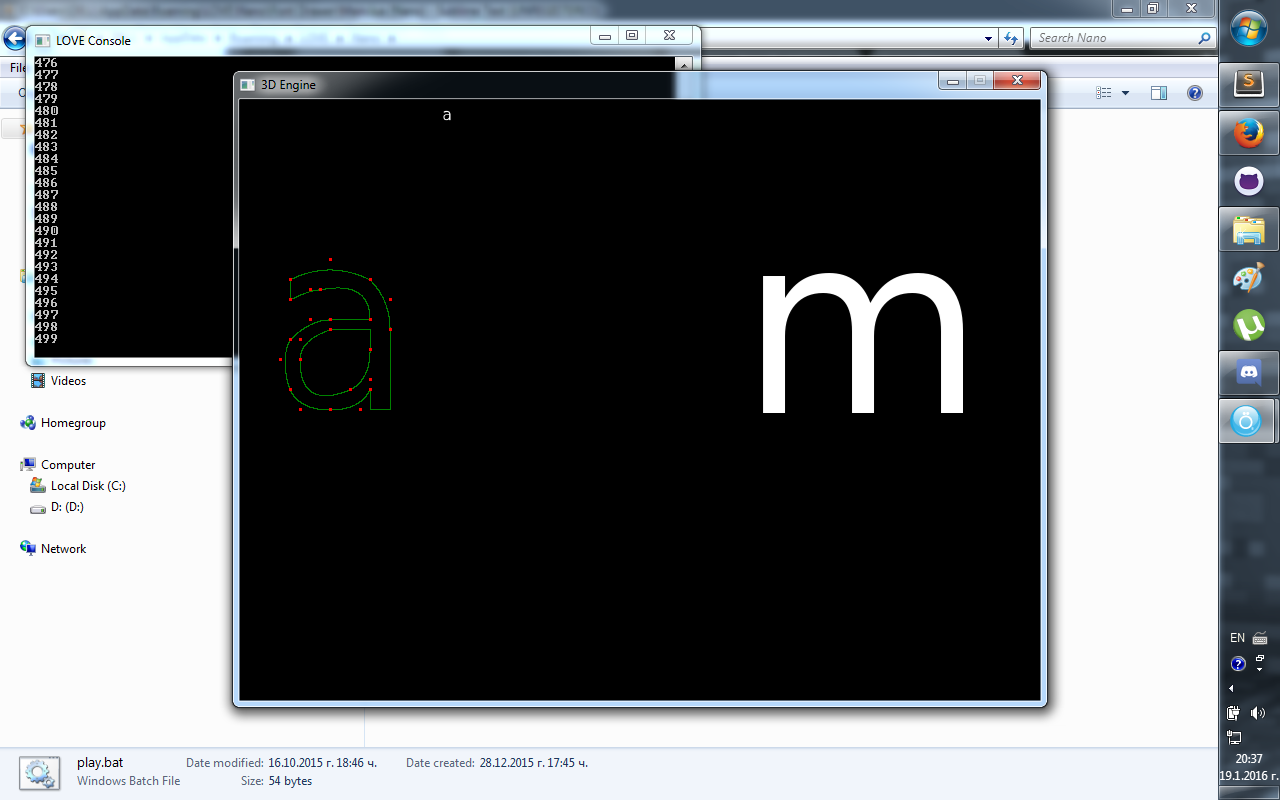
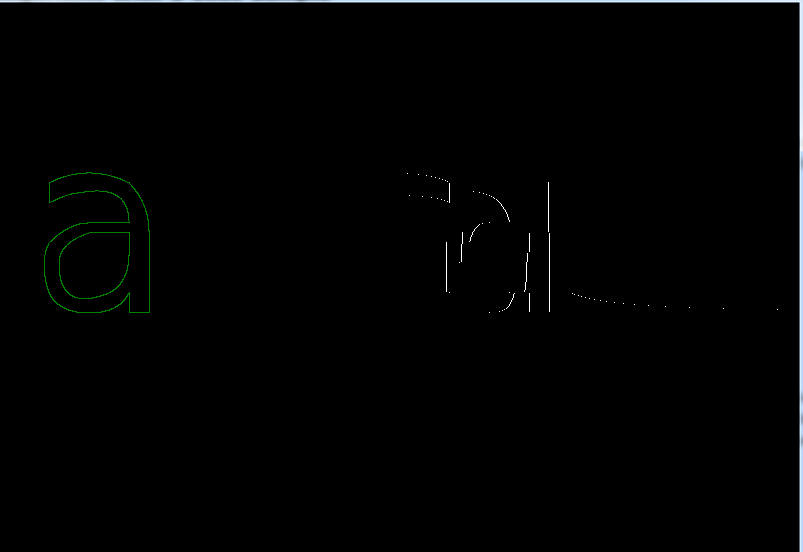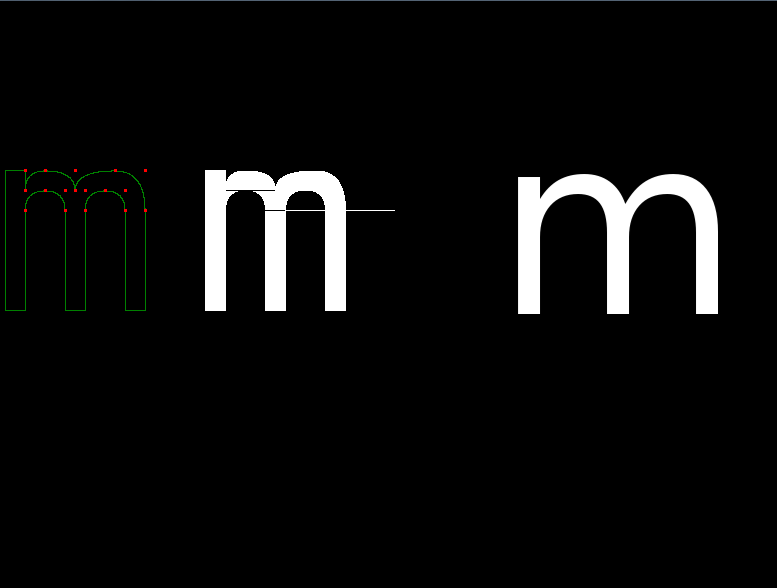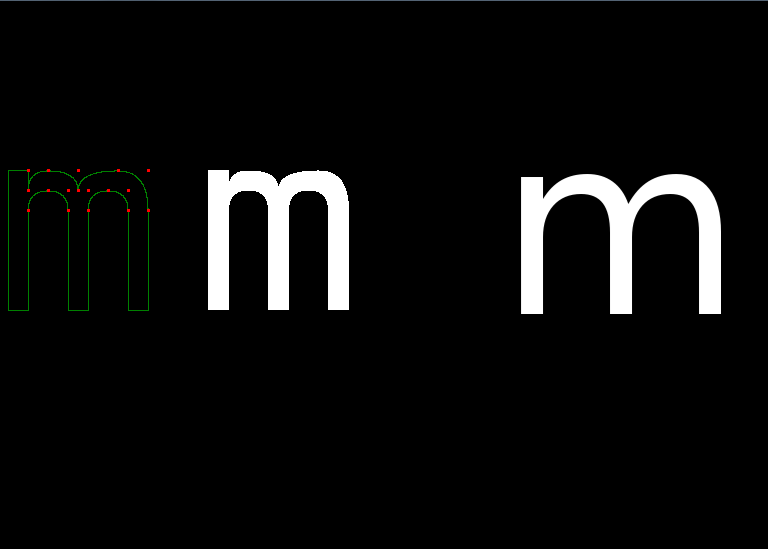during the last few days I have been experimenting with bezier curves and drawing fonts with them. At this point I can generate the path by iterating from 0 to 1 at a given interval. The result is satisfying and it works. However, for filling bezier polygons made of bezier curves and segments, I need a mathematical function that will give me the intercepts of a curve at a given y-coordinate. First, here is a comparison between both methods:
On the left side you can see an "a" generated by getting the path (the method that iterates from 0 to 1) and on the left I iterate from top to bottom and check if the beziers and segments intercept the given row. In this screenshot I have disabled the lines.
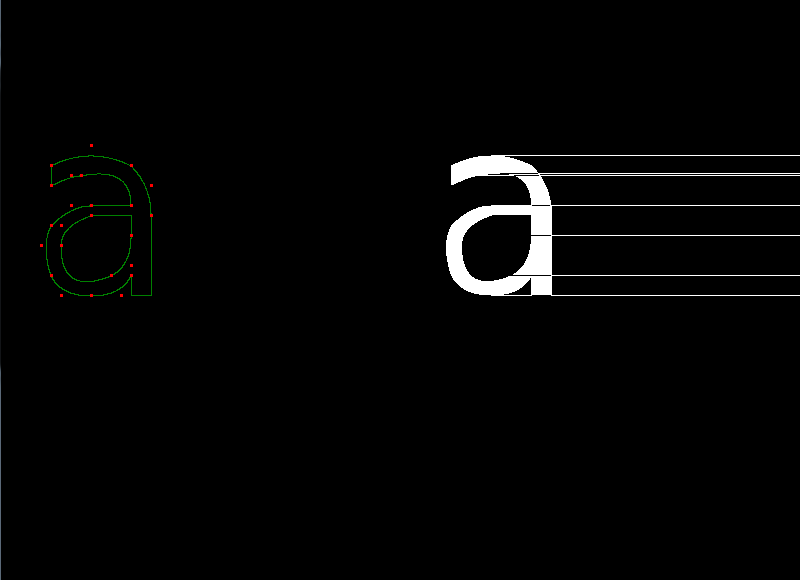
On this screenshot only the line are being rendered.
Here I render beziers and curves at the same time.
What should I do to make it generate the same form on the right and left sides?
The code I am currently using for the bezier curves.
Spoiler
Pastebin
local function Bezier(x1,y1,x2,y2,x3,y3)
--Private
local inf = 1/0
local x1 = x1
local y1 = y1
local x2 = x2
local y2 = y2
local x3 = x3
local y3 = y3
local maxY = y1 > y2 and (y1 > y3 and y1 or y3) or y2 > y3 and y2 or y3
local minY = y1 < y2 and (y1 < y3 and y1 or y3) or y2 < y3 and y2 or y3
local maxX = x1 > x2 and (x1 > x3 and x1 or x3) or x2 > x3 and x2 or x3
local minX = x1 < x2 and (x1 < x3 and x1 or x3) or x2 < x3 and x2 or x3
local xc = (x3 - 2*x2 + x1)
local xb = 2*(x2 - x1)
local yc = (y3 - 2*y2 + y1)
local yb = 2*(y2 - y1)
--Public
local self = {}
--Render
self.render = function(resolution)
local path = {}
local num = 1
for index=0, 1, 1/resolution do
path[num] = {(1-index)^2*x1+2*(1-index)*index*x2+index^2*x3, (1-index)^2*y1+2*(1-index)*index*y2+index^2*y3}
num = num + 1
end
return path
end
--Point
function self.point(index)
return {(1-index)^2*x1+2*(1-index)*index*x2+index^2*x3, (1-index)^2*y1+2*(1-index)*index*y2+index^2*y3}
end
--Get x of patricular y
function self.getX(y)
if y > maxY or y < minY then
print("Outta range!")
if y > maxY then
print("Too big")
elseif y < minY then
print("Too small")
else
print("Mkay")
end
return
elseif maxY == minY and y == minY then
return minX, maxX
end
local a = (y1 - y)
if a == 0 then
return
end
local b = yb
local c = yc
local discriminant = b^2 - 4*a*c
--print("Y: ", y)
if discriminant < 0 then
return
else
local aByTwo = 2*a
local theSQRT = math.sqrt(discriminant)
--print("Discriminant: ",discriminant)
if discriminant == 0 then
index1 = -b/aByTwo
--print("Incides (1): ",index1)
return (1-index1)^2*x1+2*(1-index1)*index1*x2+index1^2*x3
else
index1, index2 = (-b - theSQRT)/aByTwo, (-b + theSQRT)/aByTwo
--print("Incides (2): ",index1,index2)
return (1-index1)^2*x1+2*(1-index1)*index1*x2+index1^2*x3, (1-index2)^2*x1+2*(1-index2)*index2*x2+index2^2*x3
end
end
end
--Get y of patricular x
function self.getY(x)
if x > maxX or x < minX then
return
end
if maxX == minX and x == minX then
return minY, maxY
end
local index1, index2, buffer1, buffer2
local a = (x1 - x)
if a == 0 then
return
end
local b = xb
local c = xc
local discriminant = b^2 - 4*a*c
if discriminant < 0 then
return
else
local aByTwo = 2*a
local theSQRT = math.sqrt(discriminant)
if discriminant == 0 then
local index1 = -b/aByTwo
return (1-index1)^2*y1+2*(1-index1)*index1*y2+index1^2*y3
else
local index1, index2 = (-b - theSQRT)/aByTwo, (-b + theSQRT)/aByTwo
return (1-index1)^2*y1+2*(1-index1)*index1*y2+index1^2*y3, (1-index2)^2*y1+2*(1-index2)*index2*y2+index2^2*y3
end
end
end
--Scanline render
function self.scanRender()
local path = {}
local counter = 1
local fX, sX
local a = (y3 - 2*y2 + y1)
local b = 2*(y2 - y1)
for i=minY, maxY do
fX, sX = self.getX(i,a,B)/>/>/>
if fX then
path[counter] = fX
path[counter+1] = i
counter = counter + 2
if sX then
path[counter] = sX
path[counter+1] = i
counter = counter + 2
end
end
end
return path
end
--More efficient
--Self
return self
end
The code used for segments:
Spoiler
Pastebin
local function Segment(x1,y1,x2,y2)
--Private
local x1 = x1
local x2 = x2
local y1 = y1
local y2 = y2
local maxX = x1 > x2 and x1 or x2
local minX = x1 < x2 and x1 or x2
local maxY = y1 > y2 and y1 or y2
local minY = y1 < y2 and y1 or y2
--Public
local self = {}
function self.render(resolution)
local path = {}
for i=0,1,1/resolution do
path[#path + 1] = {x1*(1-i)+x2*i, y1*(1-i)+y2*i}
end
return path
end
--get x
function self.getX(y)
index = (y - y1)/(y2 - y1)
if index <= 1 and index >= 0 then
local toret = x1 + index*(x2 - x1)
return toret
end
end
--get y
function self.getY(x)
index = (x - x1)/(x2 - x1)
if index <= 1 and index >= 0 then
return y1 + index*(y2 - y1)
end
end
--scanLine
function self.scanRender()
local path = {}
local counter = 1
for i=minY, maxY do
path[counter] = self.getX(i)
path[counter + 1] = i
counter = counter + 2
end
return path
end
--Constructor
return self
end
And the code I use for the drawing itself:
Spoiler
Pastebin
love.graphics.setCanvas(can)
local xBuffer = {}
local state = false
for i=0,500 do
for k,v in pairs(beziers) do
a,b = v.getX(i)
--print(a, type(a))
--print(b, type(B)/>/>/>)
if a then
xBuffer[round(a)] = 1
if b then
xBuffer[round(a)] = 1
end
end
end
for k,v in pairs(lines) do
a = v.getX(i)
--print(a, type(a))
if a then
xBuffer[round(a)] = 1
end
end
state = false
for x=0,600 do
if xBuffer[x] then
--state = not state
love.graphics.points(x,i)
end
if state then
--love.graphics.points(x,i)
end
end
end
love.graphics.setCanvas()
Finally, a special note to Bomb Bloke. I used this website.
Thanks in advance guys!
Edit: Please go the 10th answer.
Edited on 19 January 2016 - 02:05 PM
