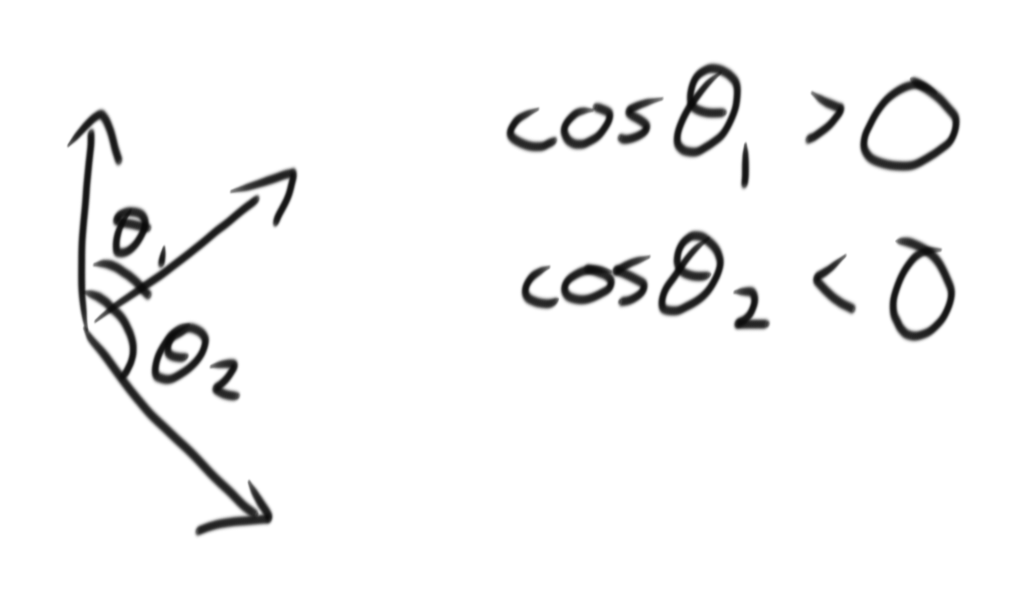- Resolved - 3D Rendering Optimization (polygon facing direction)

So, I've been working on a 3D renderer:
http://www.computerc...-rendering-api/
http://www.computerc...48-3d-renderer/

Here's a GIF (Real time ; Not sped up):


I'd like to optimize the performance by not rendering as many polygons, because the lag starts kicking in as soon as more polygons are rendered. Bomb Bloke recommended that I should only render polygons if they are facing towards the camera.

Does anyone know how I can pull this off? Do I need to save the "front" of a polygon inside the model file? How do I detect which way it is from the camera?

For example:

local cameraX
local cameraY -- Y is the height just like in MC
local cameraZ
local model = {
  {x1 = ..., y1 = ..., z1 = ..., x2 = ..., y2 = ..., z2 = ..., x3 = ..., y3 = ..., z3 = ..., color = ...}; -- This is one of the vertices in the model
  {x1 = ..., y1 = ..., z1 = ..., x2 = ..., y2 = ..., z2 = ..., x3 = ..., y3 = ..., z3 = ..., color = ...};
  {x1 = ..., y1 = ..., z1 = ..., x2 = ..., y2 = ..., z2 = ..., x3 = ..., y3 = ..., z3 = ..., color = ...};
  {x1 = ..., y1 = ..., z1 = ..., x2 = ..., y2 = ..., z2 = ..., x3 = ..., y3 = ..., z3 = ..., color = ...};
}

An object can be loaded at oX, oY, oZ with one of the loaded models.

It might be worth finding out how OpenGL does this stuff.

Lupus590, on 01 September 2017 - 03:31 PM said:

It might be worth finding out how OpenGL does this stuff.

Hm. I just searched a bit and I can't find a clear example or explenation. If you know about one, would you like to give me a link?

You can use the dot product! Dot products are awesome. It returns the cosine of the angle between two vectors. That might not mean anything on its own, but it's insanely useful because…
The angle between the vectors will be between 0 and 180 degrees. The cosine of an angle less than 90 degrees will be positive, and greater than 90 degrees will be negative.

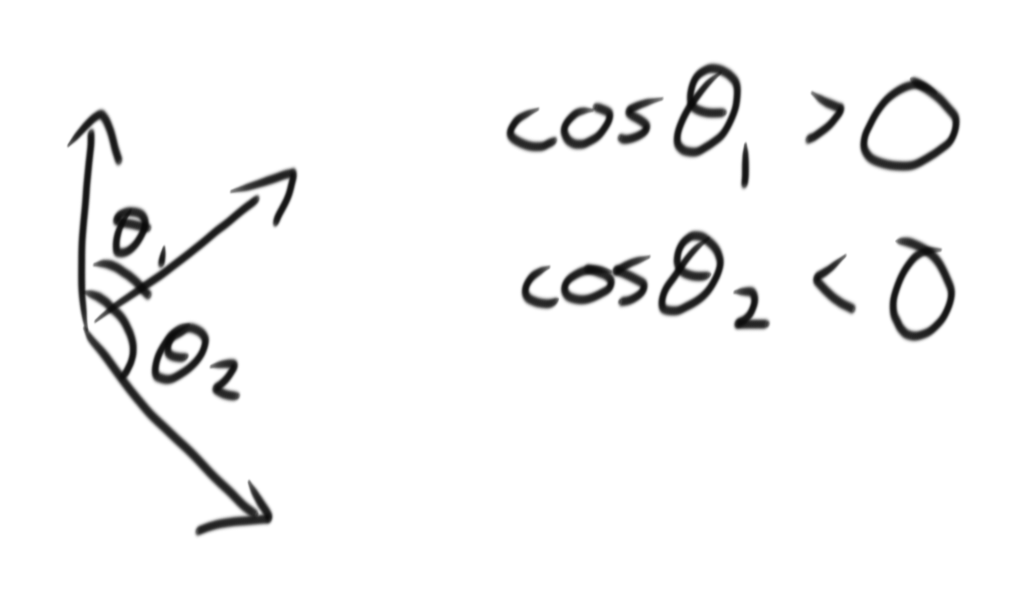
You can use this to tell if two vectors are facing the same direction. If the cosine of the angle between them (the dot product) is positive, then they are, otherwise, they aren't.
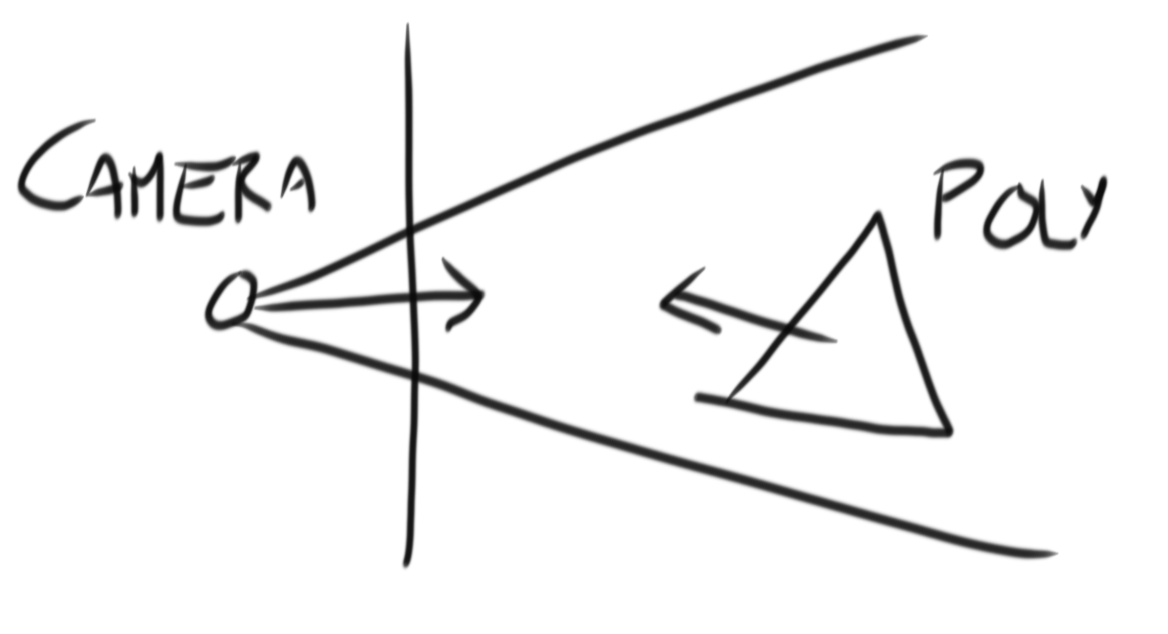
So, you can use this with the unit vector of the camera's facing direction (probably (0, 0, 1) or (0, 0, -1) for you), and the normal vector of the polygon (I'll explain how to calculate this in a bit), to work out whether the polygon is facing the camera. However, you'll want to make sure that the dot product is negative because you're checking if they're pointing towards each other, not in the same direction:

So, time for the normal vector of a polygon. The cross product this time. Basically, A x B gives you a vector perpendicular to both A and B. You can use two edges of the triangle of your polygon for A and B, just note that they both must originate from the same point.

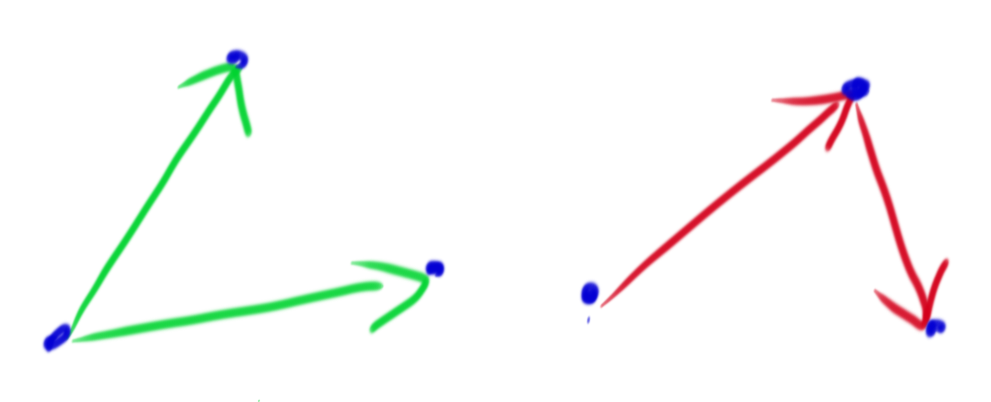
Normalise this (make it a unit vector (divide it by its length)), and you have a normal unit vector (normal vector of the polygon). However… the order matters here. A x B is different to B x A, because there will be two perpendicular vectors to the plane defined by A and B (opposite in direction).

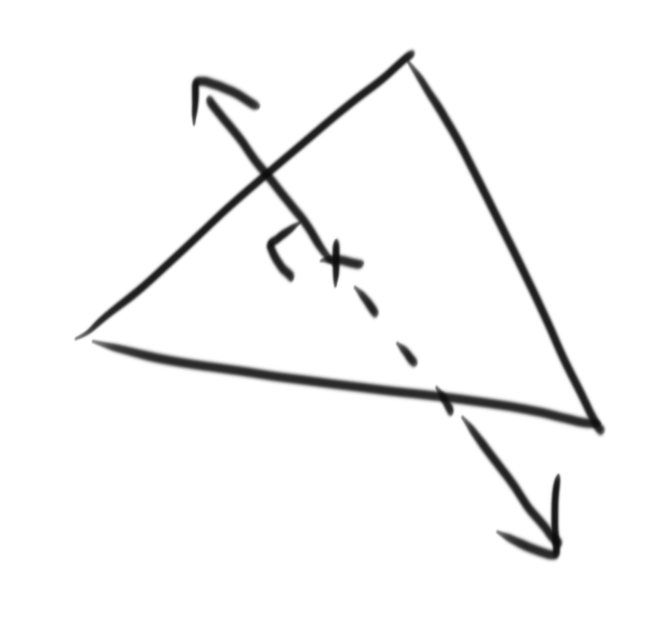
If I recall correctly, this means that you must define the points in your polygon in an anticlockwise manner, so if you had all 3 points with the same Z, they'd go anticlockwise to face the camera. It might be clockwise instead though, experiment a little and you'll find out very quickly. You can always stick a few negatives in places to fix it as well, so basically just be consistent.
The CC vector library has the dot and cross product built in, or you can write your own.

My explanations when it comes to maths are appalling, so do ask if any (or all) of this makes no sense. I've assumed a decent understanding of vectors as you're playing with 3D, but who knows, you might have no clue. I learnt all this from a GODOT tutorial, so take a look.

Note: The dot product is actually the cosine of the angle multiplied by the magnitude of both vectors, but use unit vectors so the magnitude of both are 1 and therefore can be ignored.

First: +1 for all the effort :)/>
Second: So..
I need a negative dot product for the polygon to start rendering?
And the dot product is calculated with the cosine of the angle multiplied by the magnitude of both vectors?
But which vectors are we talking about exactly? The one from the camera and one from a corner of a polygon?

Xelostar, on 01 September 2017 - 07:03 PM said:

But which vectors are we talking about exactly? The one from the camera and one from a corner of a polygon?

Given a triangle ABC, you take the dot product between vectors AB and BC. The triangle must be in view space though (so transformed, ready for rendering). I haven't looked at your rendering code, so I'm not sure what you're doing behind the scenes.

Xelostar, on 01 September 2017 - 07:03 PM said:

First: +1 for all the effort :)/>
Second: So..
I need a negative dot product for the polygon to start rendering?
And the dot product is calculated with the cosine of the angle multiplied by the magnitude of both vectors?
But which vectors are we talking about exactly? The one from the camera and one from a corner of a polygon?

Oh right, there are two ways of calculating the dot product, one of which is the sum of the product of each component (done by the vector library), but that's equivalent to the magnitude of each vector multiplied by the cosine of the angle. The sign (not sine) of the angle is what you want, so the sign of the dot product is what you want, which can be done easily with the vector library.
The vectors you want are the direction of the camera (probably (0, 0, 1) or (0, 0, -1) if the camera is fixed, facing forwards) and the normal vector of the polygon (calculated with the cross product).

But it's easiest to use the sum of the product between the vectors?
How do I exactly calculate this?
What do I use the two edges of a polygon for?

I'm sorry for all the questions, I'm not a professional at all. :P/>

So, the dot product is defined as the cosine of the angle between two vectors multiplied by their magnitude, and also as the sum of products of the components of the vector. This means you can calculate the dot product, and use that to determine the cosine of the angle, as the two are equivalent (with two unit vectors). The native vector library has a :dot() method so you don't need to worry about the details, although it's something like this:

local function dot(a, B)/>
    return a.x * b.x + a.y * b.y + a.z * b.z
end

The edges of the polygon are for finding the normal vector to the polygon, which is then used to determine where it's facing. You use the cross product of the two edge's vectors to find the normal vector.

Np with asking questions, this is AAP after all.

So there are two ways of calculating the dot product. I can calculate it in one way and use the other way to determine the orientation? Am I right?
If so, would you be able to mathematically write down the formulas?
I know how th dot product is calculated using the coordinates of two vectors, but I just need to know the other one.
Also: this way we're not two sides of the polygon? Where does that come in?

Watch bennybox's software rendering tutorial on youtube. He goes very in-depth on how to things such as face culling, screen space clipping, etc.

(I didn't see the reply. Sorry for the late answer)

I'd like to watch it, but sadly I don't have a lot of time and patience :P/>
Also, as you might no know, I'm using rasterization to render the 3D images. (Which isn't too professional)
That's why clipping is not going to work and the tutorial might not be too useful for me. :/
I'm just trying to understand some optimization techniques that I'd be able to use with rasterization like not rendering a polygon if it's facing the other direction. =)

https://en.wikipedia...i/Rasterisation - see Clipping and Backface culling.

Not rendering a polygon if it's facing the other direction is backface culling, and the best way to do it is to use dot products, either with the 3D face, or once you've converted the 3D coordinates of whatever polygon you're drawing into 2D screen coordinates.

I've described the 3D process above. The 2D approach could work something like this:

local function rotate90(vector)
	return {x = -vector.y, y = vector.x}
end

local function dot(a, B)/>/>
	return a.x * b.x + a.y * b.y
end
local function isFacingCamera(pointA, pointB, pointC)
	local dirAB = pointB - pointA
	local dirBC = pointC - pointB

	return dot(rotate90(dirAB), dirBC) < 0
end

Using this, you'll have to define the points in your polygons clockwise. When they're drawn to the screen, if the polygon is facing forwards, the points will still be clockwise, and otherwise, they'll be anticlockwise. That function checks that the 3 points are clockwise. I've written `pointB - pointA` and `pointC - pointB` for simplicity, if your vectors don't have metatables with __sub then that's just `{x = a.x - b.x, y = a.y - b.y}`

Exerro, on 14 November 2017 - 07:01 PM said:

https://en.wikipedia...i/Rasterisation - see Clipping and Backface culling.

Not rendering a polygon if it's facing the other direction is backface culling, and the best way to do it is to use dot products, either with the 3D face, or once you've converted the 3D coordinates of whatever polygon you're drawing into 2D screen coordinates.

I've described the 3D process above. The 2D approach could work something like this:

local function rotate90(vector)
	return {x = -vector.y, y = vector.x}
end

local function dot(a, B)/>/>/>
	return a.x * b.x + a.y * b.y
end
local function isFacingCamera(pointA, pointB, pointC)
	local dirAB = pointB - pointA
	local dirBC = pointC - pointB

	return dot(rotate90(dirAB), dirBC) < 0
end

Using this, you'll have to define the points in your polygons clockwise. When they're drawn to the screen, if the polygon is facing forwards, the points will still be clockwise, and otherwise, they'll be anticlockwise. That function checks that the 3 points are clockwise. I've written `pointB - pointA` and `pointC - pointB` for simplicity, if your vectors don't have metatables with __sub then that's just `{x = a.x - b.x, y = a.y - b.y}`

Thanks! That's pretty easy to understand! I'll definitely try to implement it! (Will mean people have to remake their models. Especially if they have one polygon from which they want you to see both sides, but I guess I could have a variable to make it always render (and not depend on which side you're looking at))